Ejemplos de balance Ruffini

El balance Ruffini, que también se lo conoce como “Regla de Ruffini”, es una forma rápida de calcular la división de un polinomio entre un binomio del tipo  (x—r). Fue descubierto por Paulo Ruffini, un matemático, en el año 1816. El balance permite encontrar las raíces del polinomio cuando el divisor es un factor lineal.

Gracias al balance Ruffini, una vez que se localizaron las raíces del polinomio, se puede realizar la factorización en diferentes binomios como (x—r) mientras que r sea un número entero y siempre y cuando sea coherente.

Cómo resolver un algoritmo con el balance Ruffini

Como explicamos anteriormente, la regla de Ruffini es una manera de dividir un polinomio como el siguiente:

P(x)= a_nxⁿ + a_n-1x^n-1+… con el binomio Q(x) = x—r

De allí se obtiene el cociente R(x)=b_n-1x^n-1 + b_n-2x^n-2…. junto con el resto s.

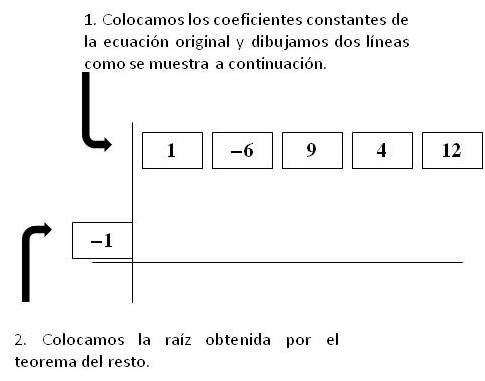
Primero se deben trazar dos líneas con los ejes de P(x) ordenados. Donde no existan términos, se debe colocar cero. Esto significa que no se deben omitir los términos que sean nulos. A continuación, del lado izquierdo se escribe la raíz r. Posteriormente se debe multiplicar a_n * r y el resultado se escribe abajo de a_n-1 para sumar los valores que se obtuvieron en la misma columna. Solo resta repetir el mismo proceso con el resto de los factores del polinomio.

Qué tener en cuenta

• El grado disminuye de 1 en 1 y cada uno de ellos termina ocupando su lugar.
• Los números de la primera columna, cuando se suman, deben ser colocados debajo del siguiente.
• Para hacer la siguiente operación, se debe multiplicar el número que está en el lado izquierdo con el resultado obtenido en la primera columna.
• En caso de que un término no se encuentre en el polinomio, el mismo debe ser remplazado por el número 0 (cero). En el caso de que no se deba poner el cero, se puede colocar cualquier otro número.
• La operación terminará cuando el resultado del ejercicio sea cero. Si esto no ocurre, se deberá repetir el mismo con otro tipo de raíz

Es importante aclarar que, aunque los polinomios no presenten el signo = y el número cero de uno de sus lados -ya que no son ecuaciones-, se deben tratar como tales al momento de resolverlas.

Ejemplo de balance Ruffini

P(x) = 3x³ + 4x² – 5

Dividido por

Q(x) = x+1